:)
와핑기법과 원근 변환 본문
이미지의 기하학적 변형
- 와핑(Warping)
- '뒤틀림', '왜곡하다'를 의미
- 영상시스템에서 말하는 Warping은 영상을 이동, 회전, 크기변환 등을 이용해 이미지를 찌그러뜨리거나 반대로 찌그러진 이미지를 복원하기 위한 처리 기법
- 변환 (Transformations)
- 좌표 x를 새로운 좌표 x`로 변환하는 함수
- 사이즈 변경(Scaling), 위치변경(Translation), 회전(Rotation) 등
(2) 유사변환(Similarity) : 크기는 변하고 각도는 보존되는 변환(ex. Scaling)
(3) 선형변환(Linear) : Vector 공간에서의 이동
(4) Affine : 선형변환과 이동변환까지 포함. 선의 수평성은 유지 (ex 사각형 -> 평행사변형)
(5) Perspective : Affine 변환에 수평성도 유지되지 않음. 원근변환.

Translation 변환
- 평행이동
- 이미지를 이동하려면 원래 있던 좌표에서 이동시키려는 거리만큼 더하면 됨.
- x_new = x_old + d1
- y_new = y_old + d2
- 이미지를 이동하려면 원래 있던 좌표에서 이동시키려는 거리만큼 더하면 됨.

- dst = cv2.warpAffine(src, matrix, dsize, dst, flags, borderMode, borderValue)
- matrix : 2X3 변환 행렬, dtype = float32
- dsize : 결과 이미지의 크기(width, height)
- dst(optional)
- flags(optional) : 보간법 알고리즘 플래그
- cv2.INTER_LINEAR : default 값. 인접한 4개 픽셀 값에 거리 가중치 사용
- cv2.INTER_NEAREST : 가장 가까운 픽셀 값 사용
- cv2.INTER_AREA : 픽셀 영역 관계를 이용한 재샘플링
- cv2.INTER_CUBIC : 인접한 16개 픽셀 값에 거리 가중치 사용
- borderMode(optional) : 외곽영역 보정 플래그
- cv2.BORDER_CONSTANT : 고정 색상 값
- cv2.BORDER_REPLICATE : 가장자리 복제
- cv2.BORDER_WRAP : 반복
- cv2.BORDER_REFLECT : 반사
- borderValue(optional) : 외곽영역 보정 플래그가 cv2.BORDER_CONSTANT 일 경우 사용할 색상 값 (default=0)
import cv2
import numpy as np
img = cv2.imread('girl.png')
rows,cols = img.shape\[0:2\]
dx, dy = 100, 50
#변환 행렬 생성
mtrx = np.float32(\[\[1, 0, dx\],
\[0, 1, dy\]\])
dst = cv2.warpAffine(img, mtrx, (cols+dx, rows+dy))
# 탈락된 외곽 픽셀을 파랑색으로 보정
dst2 = cv2.warpAffine(img, mtrx, (cols+dx, rows+dy), None,
cv2.INTER\_LINEAR, cv2.BORDER\_CONSTANT, (255,0,0) )
# 탈락된 외곽 픽셀을 원본을 반사 시켜서 보정
dst3 = cv2.warpAffine(img, mtrx, (cols+dx, rows+dy), None,
cv2.INTER\_LINEAR, cv2.BORDER\_REFLECT)
cv2.imshow('original', img)
cv2.imshow('trans', dst)
cv2.imshow('BORDER\_CONSTATNT', dst2)
cv2.imshow('BORDER\_REFLECT', dst3)
cv2.waitKey(0)
cv2.destroyAllWindows()
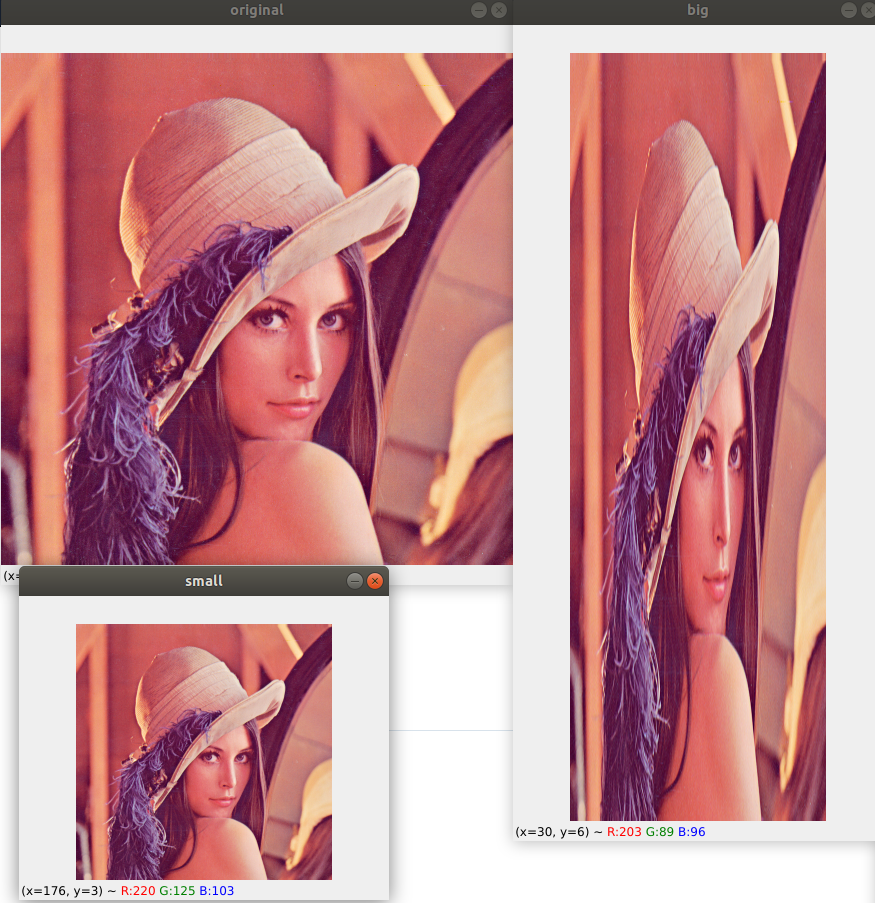
확대축소
- 일정 비율로 확대 및 축소
- 기존 좌표에 특정 값을 곱함.

import cv2
import numpy as np
img = cv2.imread('girl.png')
height, width = img.shape[0:2]
m_small = np.float32([[0.5, 0, 0],
[0, 0.5, 0]])
m_big = np.float32([[2, 0, 0],
[0, 2, 0]])
dst1 = cv2.warpAffine(img, m_small, (int(height*0.5), int(width*0.5)))
# 보간법 적용한 축소
dst2 = cv2.warpAffine(img, m_small, (int(height*0.5), int(width*0.5)), \
None, cv2.INTER_AREA)
dst3 = cv2.warpAffine(img, m_big, (int(height*2), int(width*2)))
# 보간법 적용한 확대
dst4 = cv2.warpAffine(img, m_big, (int(height*2), int(width*2)), \
None, cv2.INTER_CUBIC)
cv2.imshow("original", img)
cv2.imshow("small", dst1)
cv2.imshow("small INTER_AREA", dst2)
cv2.imshow("big", dst3)
cv2.imshow("big INTER_CUBIC", dst4)
cv2.waitKey(0)
cv2.destroyAllWindows()크기 조정 OpenCV 함수
- cv2.resize(src, dsize, dst, fx, fy, interpolation)
- dsize : 출력 영상 크기(확대/축소 목표 크기), 생략하면 fx, fy 배율을 적용
- fx, fy : 크기 배율, dsize가 주어지면 dsize를 우선 적용
- interpolation : 보간법 알고리즘 선택 플래그 (cv2.warpAffine()과 동일)
- 확대/축소를 몇 픽셀로 할지 혹은 어떤 배율로 할지 선택 가능
- dsize는 확대/축소를 원하는 목표 이미지의 크기
- fx, fy는 변경할 배율
- fx=2, fy=0.5 이면 x축으로 2배, y축으로 0.5배로 스케일링 한다는 뜻
회전

import cv2
import numpy as np
img = cv2.imread('girl.png')
rows,cols = img.shape[0:2]
# 회전 각조를 라디안 값으로 변경
d45 = 45.0 * np.pi / 180
d90 = 90.0 * np.pi / 180
# 45도 회전 행렬 (rows//2, cols//4 --> 회전축의 중심을 옮길때)
m45 = np.float32( [[ np.cos(d45), -1* np.sin(d45), rows//2],
[np.sin(d45), np.cos(d45), -1*cols//4]])
# 90도 회전 행렬
m90 = np.float32( [[ np.cos(d90), -1* np.sin(d90), rows],
[np.sin(d90), np.cos(d90), 0]])
r45 = cv2.warpAffine(img,m45,(cols,rows))
r90 = cv2.warpAffine(img,m90,(cols,rows))
cv2.imshow("origin", img)
cv2.imshow("45", r45)
cv2.imshow("90", r90)
cv2.waitKey(0)
cv2.destroyAllWindows()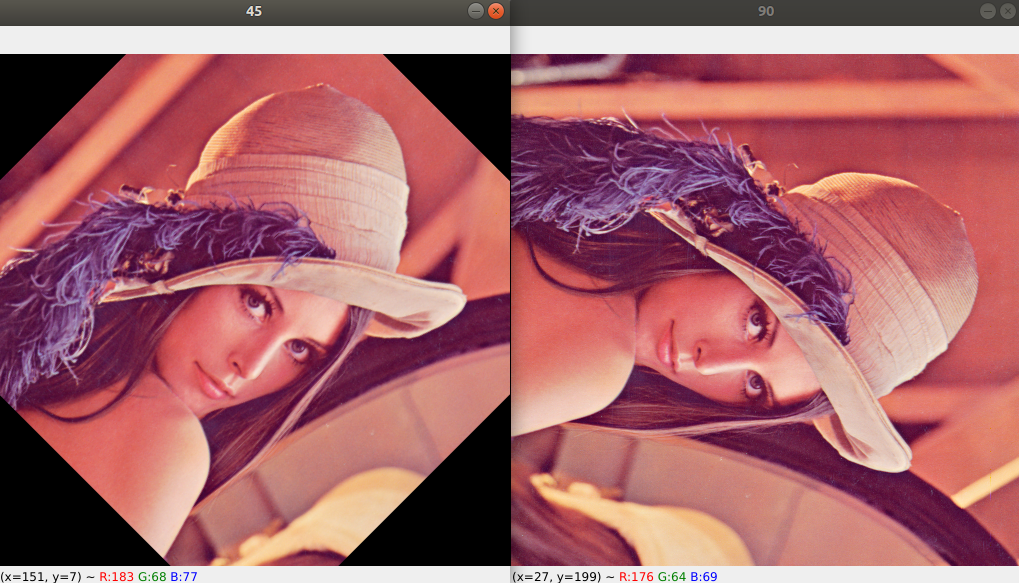
회전 행렬 구하는 OpenCV 함수
- mtrx = cv2.getRotationMatrix2D(center, angle, scale)
- center : 회전축 중심 좌표(x,y)
- Angle : 회전할 각도, 60진법
- Scale : 확대 및 축소비욜
- 회전 축을 정하고 + 회전 각도를 정하고, 확대/축소를 정ㅎㄹ 수 있음
- 복합적인 행렬 만들기 가능
import cv2
import numpy as np
img = cv2.imread('girl.png')
rows,cols = img.shape[0:2]
# 회전축은 중앙, 45도 회전, 0.5배 축소 행렬
m45 = cv2.getRotationMatrix2D((cols/2,rows/2),45,0.5)
print(m45)
# 회전축은 중앙, 90도 회전, 1.5배 확대 행렬
m90 = cv2.getRotationMatrix2D((cols/2,rows/2),90,1.5)
print(m90)
r45 = cv2.warpAffine(img, m45,(cols, rows))
r90 = cv2.warpAffine(img, m90,(cols, rows))
cv2.imshow("origin", img)
cv2.imshow("45", r45)
cv2.imshow("90", r90)
cv2.waitKey(0)
cv2.destroyAllWindows()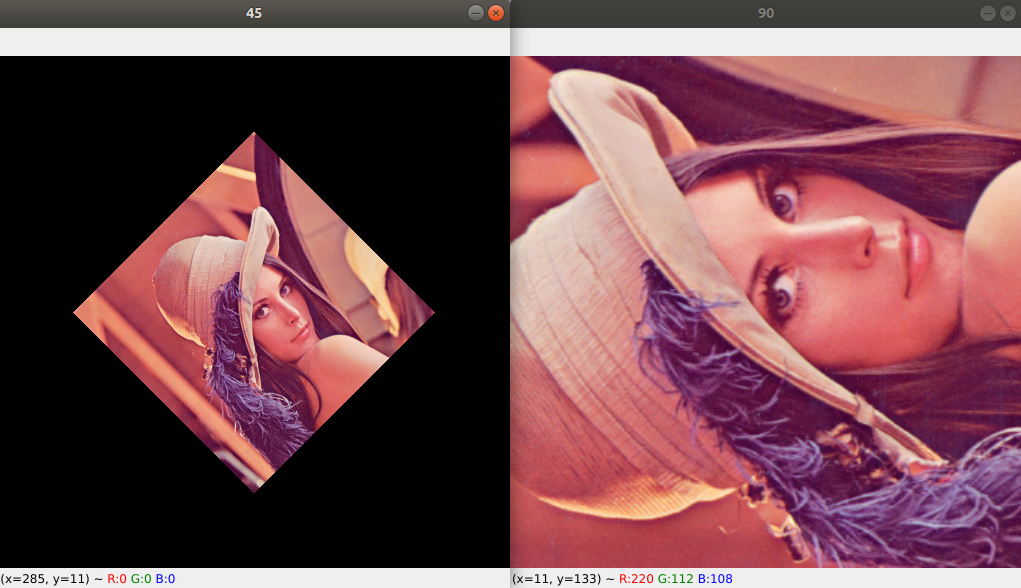
아핀 변환 - Affine
- Affine 변환 : 크기변환, 이동변환, 회전변환에서도 원래 평행했던 특성을 그래도 유지
- Affine 변환 행렬 : cv2.getAffineTransform 함수를 통해서 얻을 수 있음. 2X3 행렬
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('chess.png')
rows,cols = img.shape[0:2]
# 변환전 3개 점의 좌표
pts1 = np.float32([[50,50],[200,50],[50,200]])
# 변환 후 3개 점의 좌표
pts2 = np.float32([[10,100],[200,50],[100,250]])
# 기존 점이 새로운 점으로 이동시킬 때 필요한 행렬 찾기
M = cv2.getAffineTransform(pts1,pts2)
print(M)
# 구해진 행렬을 적용하여 이미지 변환
dst = cv2.warpAffine(img,M,(cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('Input')
plt.subplot(122),plt.imshow(dst),plt.title('Output')
plt.show()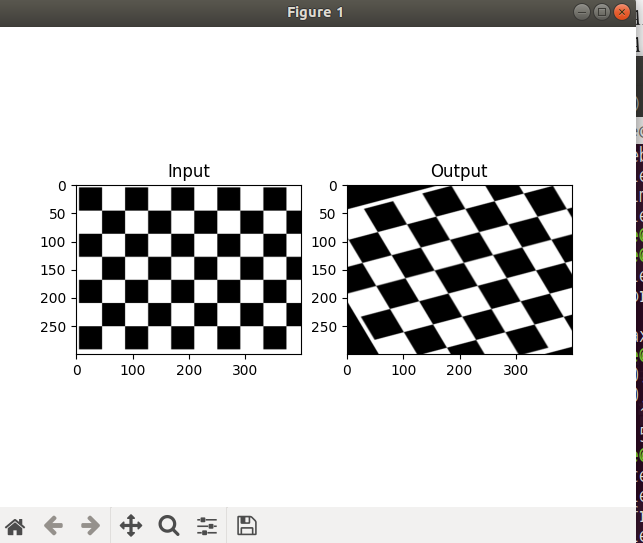
원근 변환 - Perspective
- Perspective 변환
- 원근법을 적용한 변환
- 직선의 성질만 유지 되고, 선의 평행성은 유지되지 않는 변환
- 기차길은 서로 평행하지만 원근변환을 거치면 평행성은 유지되지 못하고 하나의 점에서 만나는 것처럼 보임
- 반대의 변환도 가능 -> 차선 추출에 사용
- Perspective 변환 행렬
- cv2.getPerspectiveTransform 함수를 통해 얻을 수 있음
- 이동할 4개 점의 좌표가 필요
- 결과값은 3X3 행렬
- cv2.warpPerspective() 함수에 변환 행렬값을 적용해서 이미지 변환
import cv2
import numpy as np
from matplotlib import pyplot as plt
img = cv2.imread('chess.png')
rows,cols = img.shape[0:2]
# 변환전 4개 점의 좌표
pts1 = np.float32([[20,20],[20,280],[380,20],[380,280]])
# 변환 후 4개 점의 좌표
pts2 = np.float32([[100,20],[20,280],[300,20],[380,280]])
# 4개 점의 위치에 다른 색깔로 원 그리기
cv2.circle(img, (20,20), 20, (255,0,0),-1)
cv2.circle(img, (20,280), 20, (0,255,0),-1)
cv2.circle(img, (380,20), 20, (0,0,255),-1)
cv2.circle(img, (380,280), 20, (0,255,255),-1)
# 4개 점의 이동 정보를 가지고 행렬 계산
M = cv2.getPerspectiveTransform(pts1, pts2)
print(M)
# 구해진 행렬을 적용하여 이미지 변환
dst = cv2.warpPerspective(img, M, (cols,rows))
plt.subplot(121),plt.imshow(img),plt.title('image')
plt.subplot(122),plt.imshow(dst),plt.title('Perspective')
plt.show()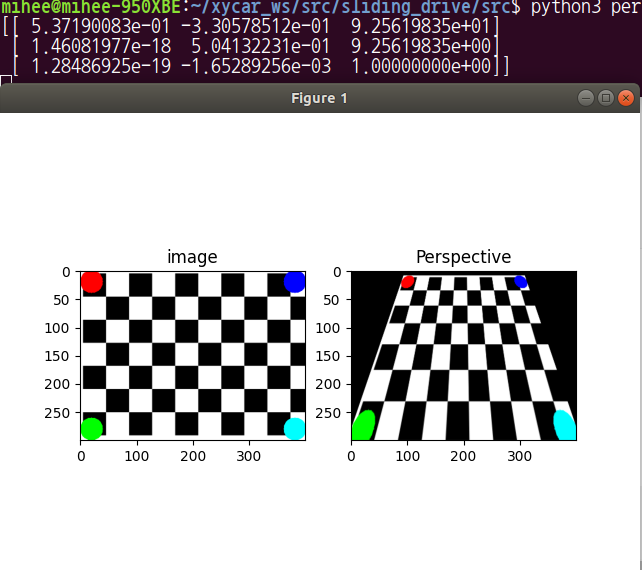
'ROS' 카테고리의 다른 글
| 슬라이딩 윈도우 기반 차선 인식 (0) | 2022.04.10 |
|---|---|
| 원근 변환과 슬라이딩 윈도우 (0) | 2022.04.10 |
| 허프변환 기반 차선인식 (0) | 2022.04.10 |
| 명도차 기반 차선 인식 (0) | 2022.03.30 |
| OpenCV 자이카 카메라 활용 (0) | 2022.03.28 |
Comments




